NOI 2023 共包括两试 6 道题目。其中，

l 第一试题目依次为：方格染色（color）、桂花树（tree）、深搜（dfs）；

l 第二试题目依次为：贸易（trade）、字符串（string）、合并书本（book）。

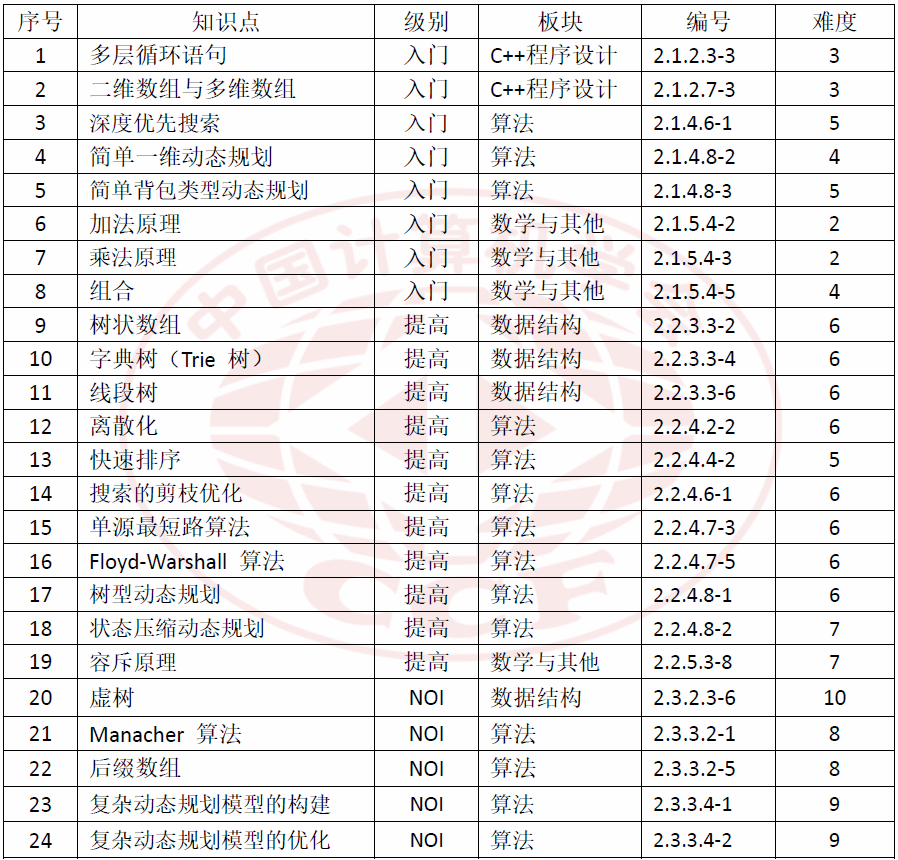
全部题目所涉及的主要知识点统计如下：

NOI 2023 题目所涉及的主要知识点

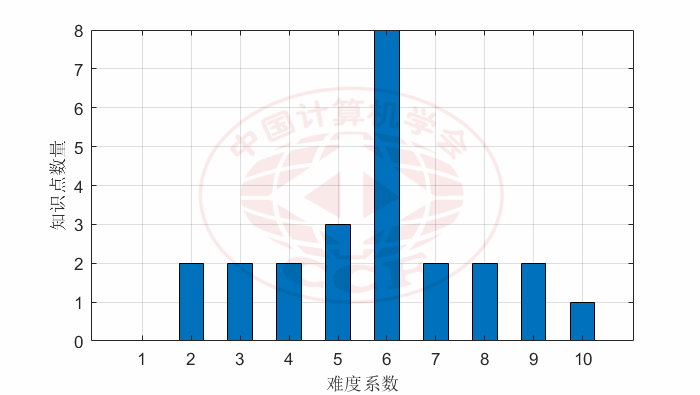
主要知识点的学习难度系数分布统计如下：

知识点难度系数统计直方图

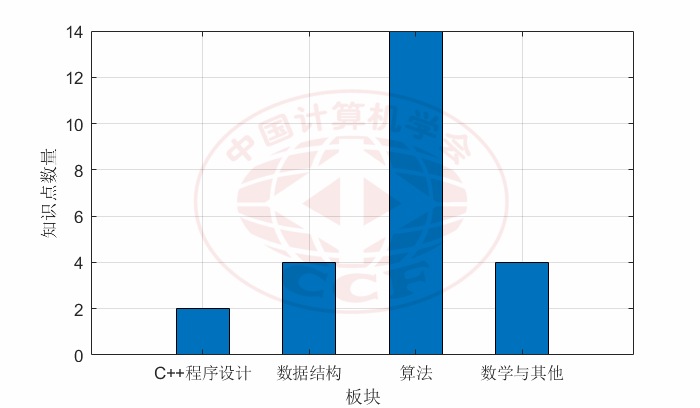
主要知识点的板块分布统计如下：

知识点板块统计直方图

总体上看，NOI 2023 所考察的主要知识点分布较广，在“级别”上以“提高级”知识点最多，在“难度”上以 6 级知识点最多，而在“板块”上则以“算法”知识点最多。主要知识点的学习难度系数，范围为从 2 到 10，与大纲的建议考察范围基本一致，而在“虚树”知识点上（大纲中学习难度系数为 10）略超出了建议范围。

以下为每道题的知识构成详细分析。

1 方格染色（D1T1）

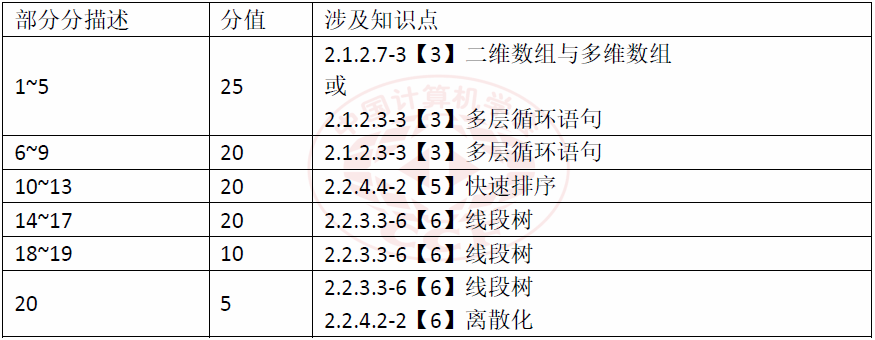
本题是整套题目中的简单题，预期绝大多数NOI选手都能得到 95 分或者 100 分。最后 5 分涉及到离散化和少量的细节处理。本题的部分分设置充足，即便选手未掌握扫描线和线段树，也应能得到 65 分左右。

本题正解所考察的知识点主要包括离散化、线段树。其中，“离散化”属于“提高级”的“算法策略”，大纲标注学习难度系数为6；“线段树”属于“提高级”的“特殊树”，大纲标注学习难度系数为6。所涉知识点难度均不超过大纲规定NOI考试所要求的难度。

此外，本题需要将“线段树”应用于扫描线，而“扫描线”知识暂未包含在现版本大纲内。建议在大纲修订时将“扫描线”知识点增加到“提高级”的“算法策略”部分，难度系数有待确定。

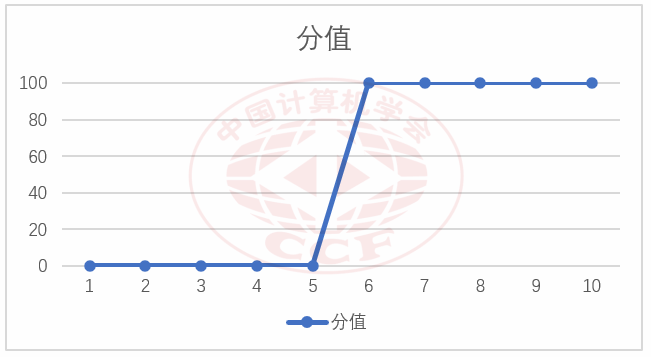
1.1 难度设置

本题的部分分所考察的知识点具体包括：

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

方格染色的难度设置曲线

1.2 总体评价

本题所考察的知识点的最高难度系数为6级（或暂列 7 级），与大纲关于NOI题目知识点难度的建议相一致，也符合D1T1的应有难度。本题的“知识点难度系数—可得分数”曲线较为平缓，说明部分分设置合理。

2 桂花树（D1T2）

本题是NOI比赛中的中等难度题目，其代码实现难度较低，但对动态规划状态设计的要求较高。本题要求选手需要具备一定的模型转化能力和问题洞察能力，能够从问题本身出发设计出合理的状态。

本题正解所考察的知识点主要包括状态压缩动态规划、复杂动态规划模型的构建。其中状态压缩动态规划属于提高级动态规划，大纲标注学习难度系数为7，复杂动态规划模型的构建属于NOI级动态规划，大纲标注学习难度系数为9，本题需要观察出复杂的树上结构，将状态压缩动态规划应用在此模型上，属于状态压缩动态规划的高级应用，综合本题难度为9，所涉知识点难度均不超过大纲规定NOI考试所要求的难度。

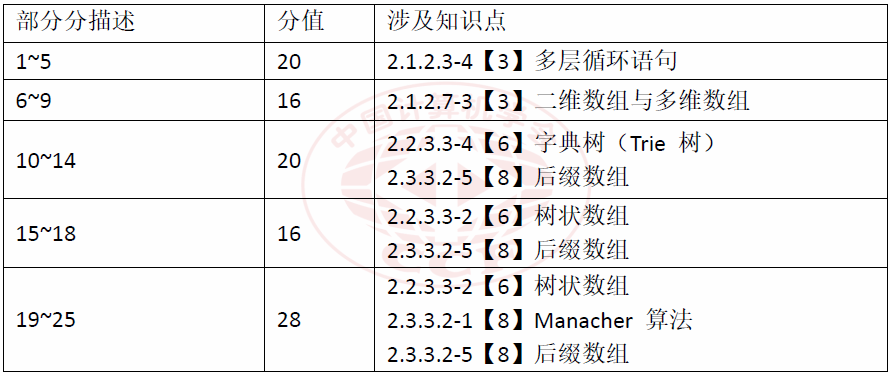
2.1 难度设置

本题的部分分所考察的知识点具体包括：

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

桂花树的难度设置曲线

2.2 总体评价

本题所考察的知识点在大纲中不超过9级，符合大纲对于NOI试题难度的预设。本题的部分分设置难度合理。

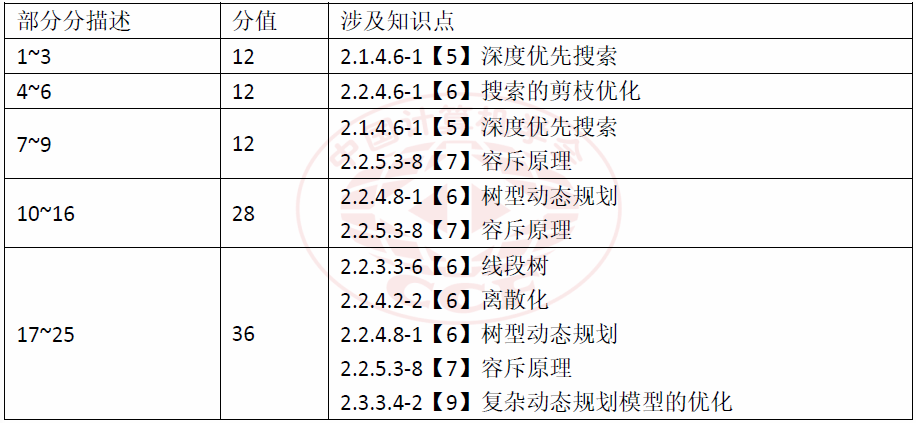
3 深搜（D1T3）

本题难度较大，要求选手具备对多个知识点的综合掌握和灵活运用能力。本题标准算法的实现细节比较复杂，代码规模为 6KB 左右，因此对选手的代码实现能力要求较高。

本题正解所考察的知识点主要包括容斥原理、复杂动态规划模型的优化。其中，容斥原理属于提高级组合数学，大纲标注学习难度系数为7，复杂动态规划模型的优化属于NOI级，大纲标注学习难度系数为9。本题需要分析DFS树的性质，将容斥原理应用在树型动态规划上，并使用线段树作为数据结构来优化动态规划的模型。综合来看，本题所涉知识点难度均不超过大纲规定NOI级比赛所要求的难度。

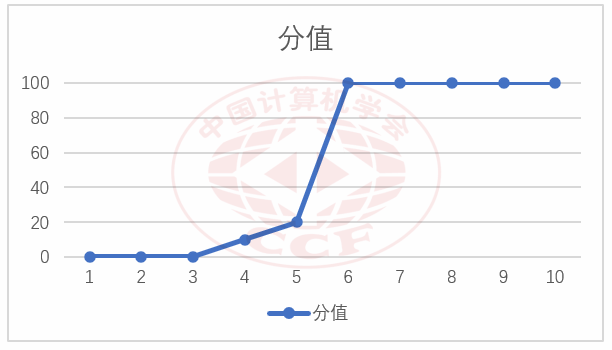
3.1 难度设置

本题的部分分所考察的知识点具体包括：

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

“深搜”的难度设置曲线

3.2 总体评价

本题所考察的知识点在大纲中不超过9级，符合大纲对于NOI试题难度的预设。本题的部分分设置难度合理。

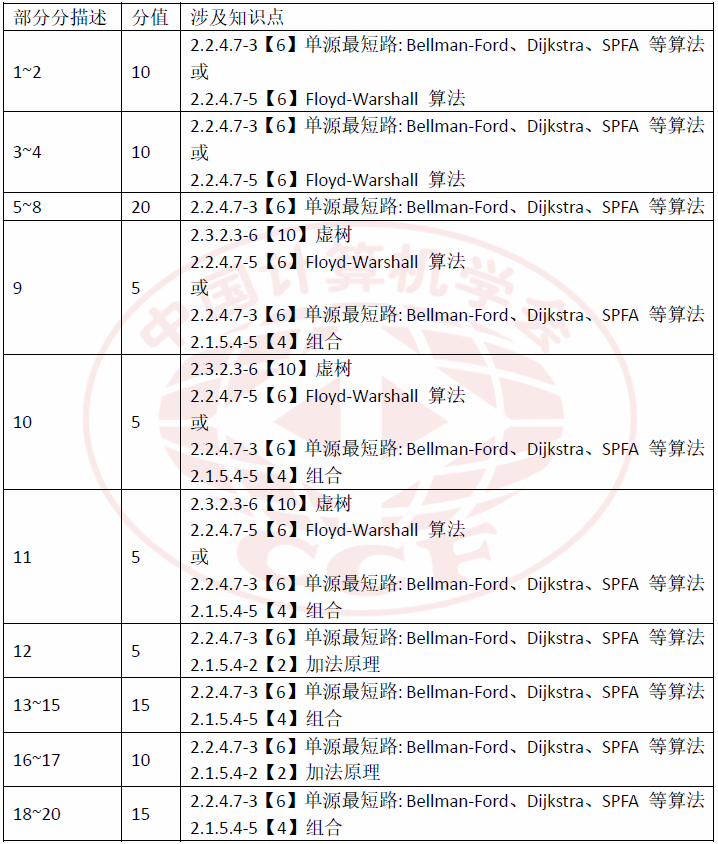
4 贸易（D2T1）

本题难度较低，且解法多样。本题主要考察选手对树形动态规划或者最短路方法的深入理解和灵活运用能力。本题部分分设置较为充足，对选手代码实现能力的要求较低。

本题正解所考察的知识点主要包括最短路径（Dijkstra）、组合。其中“最短路”属于“提高级”的“图论算法”，词条为“单源最短路：Bellman-Ford、Dijkstra、SPFA 等算法”，大纲标注学习难度系数为6；“组合”（不直接求每项，而是分类到每个节点上）属于“入门级”的“离散与组合数学”，大纲标注学习难度系数为4。除了正解以外，本题部分分上较多选手采用了涉及“虚树”的其他解法，该知识点属于“NOI级”中的“复杂树”，大纲标注学习难度系数为10。

4.1 难度设置

本题的部分分所考察的知识点具体包括：

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

“贸易”的难度设置曲线

4.2 总体评价

本题正解的知识点最高难度系数为6级，与大纲关于NOI题目知识点难度的建议相一致，符合D2T1的应有难度。

本题在部分分设置上有一定坡度，难度设置总体上比较合理，基本符合大纲对于NOI试题难度的预设。在一些部分分上，有相当数量的选手采用了知识点学习难度系数最高为10级的解法，这种解法虽然也较为自然，但对正解的启发性比较有限。

5 字符串（D2T2）

本题是属于中档难度，主要用于区分集训队与非集训队选手。本题要求选手掌握基本的字符串知识，并具备灵活使用数据结构进行计数问题优化的能力。

本题正解所考察的知识点主要包括后缀数组、Manacher 算法、二维数点（常见实现技巧为：扫描线、树状数组）。其中，“后缀数组”属于“NOI级”的“字符串算法”，大纲标注学习难度系数为 8；“Manacher 算法”属于“NOI级”的“字符串算法”，大纲标注学习难度系数为 8；“树状数组”属于“提高级”的“特殊树”，大纲标注学习难度系数为 6 。所涉及的知识点难度均不超过大纲规定的NOI考试所要求的难度。

此外，本题的“二维数点”需要通过“扫描线”来实现，“扫描线”暂未列入现版本的NOI大纲内。建议在大纲修订时将“扫描线”知识点增加到“提高级”的“算法策略”部分，难度系数有待确定。

5.1 难度设置

本题的部分分所考察的知识点具体包括：

其中“后缀数组”可以使用“二分法”与“字符串哈希函数构造”来替代，能够通过部分分测试点10-12，15-16，得到分值20； 再结合“Manacher 算法”可以通过部分分测试点 19-21，得到分值 32。

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

“字符串”的难度设置曲线

5.2 总体评价

本题所考察的知识点最高难度系数为 8 级，与大纲关于 NOI 题目知识点难度的建议相同，大致符合 D2T2的难度定位。本题的“知识点难度系数—可得分数”曲线比较平缓，说明部分分设置较为合理，并且实际上每档部分分均存在对应的优秀做法。

本题存在一些具有创新性的做法，能够有效启发选手在字符串方面的能力，是一道很好的字符串题目。

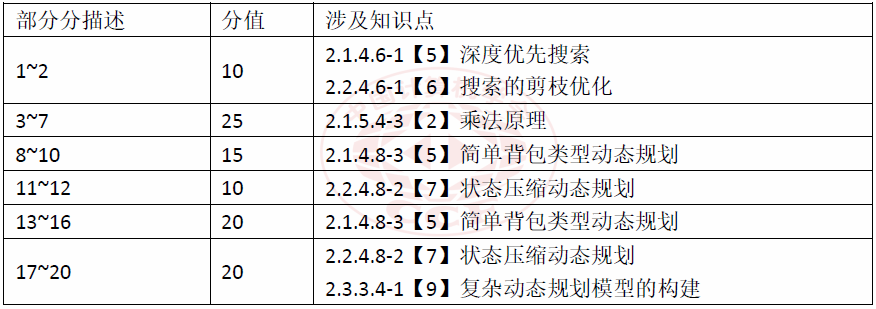
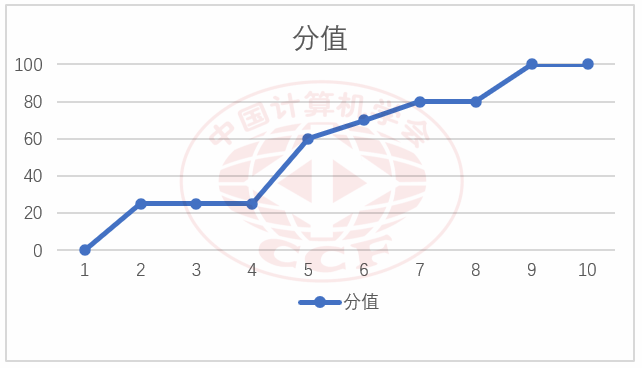
6 合并书本（D2T3）

本题的难度很大，预期绝大部分选手只能获得较低的部分分。本题要求选手能够根据搜索方式优化动态规划状态的设计，同时需要具备较强的代码实现能力。

本题正解所考察的知识点主要包括广度优先搜索、搜索的剪枝优化。其中，“广度优先搜索”属于“入门级”的“搜索算法”，大纲标注学习难度系数为5；“搜索的剪枝优化”属于“提高级”的“搜索算法”，大纲标注学习难度系数为6。所涉知识点难度均不超过大纲规定NOI考试所要求的难度。

此外，本题部分分也可以不进行搜索，使用状态压缩动态规划和简单一维动态规划两个知识点通过，这两个知识点大纲标注学习难度系数分别为 7,4，同样不超过大纲规定 NOI 考试所要求的难度。

6.1 难度设置

本题的部分分所考察的知识点具体包括：

本题的“知识点难度系数—可得分数”关系见下图（横轴为知识点难度系数，纵轴为不超过该难度的可得分数）：

“合并书本”的难度设置曲线

6.2 总体评价

本题所考察的知识点的最高难度系数为6级（或部分分做法 7 级），与大纲关于NOI题目知识点难度的建议相一致。

本题虽然最高知识难度系数低于其他题目，但是其要求的思维难度很高，是一道知识考察非常灵活的题目。本题所考察的最难知识点——搜索的剪枝优化，在大多数选手的掌握范围内，但选手必须深入地理解搜索剪枝的本质，并对特定问题进行深入分析，才能设计出优秀的剪枝策略和较好的算法。采取不同剪枝策略和不同时间复杂度的搜索算法，可以分别取得 10、65、80、90、100 等分数，阶梯设置基本平滑，说明本题的部分分设置比较合理。

报告执笔人：